Géométrie : les fondamentaux du collège

¤ Une droite se note entre parenthèses.
Exemple : (AB) désigne la droite qui passe par les points A et B.
Remarque : une droite est illimitée.
Propriété : par deux points ne passe qu’une seule droite.

¤ Un segment se note entre crochets.
Exemple : [AB] désigne le segment de droite d’extrémités A et B.

¤ Une demi-droite se note entre un crochet et une parenthèse.
Exemple : [AB) désigne la demi-droite d’origine A passant par B.

¤ Une distance se note sans rien.
Exemple : AB désigne la distance entre les points A et B, c’est-à-dire la longueur du segment [AB].

¤ Deux droites qui se coupent en formant un angle droit sont dites perpendiculaires.
On utilise alors le symbole $\perp$
Exemple : (AB) $\perp$ (CD)

¤ Deux droites qui ne sont pas sécantes sont dites parallèles.
On utilise alors le symbole //.
Exemple : (AB) // (CD)

¤ Le symbole $\in$ signifie "appartient à"
Exemple : A $\in$ (BC) signifie que le point A est situé sur la droite (BC)
Remarque : A $\notin$ (EF) signifie que le point A n’appartient pas à la droite (EF).

¤ Pour nommer un polygone, on cite les sommets en "tournant" autour de la figure et on n’utilise ni parenthèses ni crochets ni accolades.
Exemples : Le triangle ABC, le quadrilatère MATH

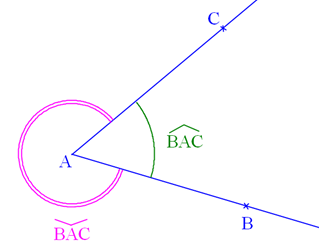
¤ Deux demi-droites [AB) et [AC) définissent deux angles géométriques :
l’angle saillant $\widehat{BAC}$ dont la mesure est comprise entre 0° et 180°
l’angle rentrant $\check{BAC}$ dont la mesure est comprise entre 180° et 360°

¤ Deux angles opposés par le sommet ont la même mesure.
Exemple : $\alpha$ = $\beta$

¤ Les deux angles roses définis ci-dessous par les deux droites d et d’ et leur sécante $\Delta$ sont dits correspondants.

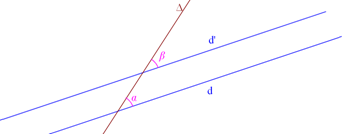
Si d // d’ alors $\alpha$ = $\beta$
Réciproquement, si $\alpha$ = $\beta$ , alors d // d’
¤ Les deux angles verts définis ci-dessous par les deux droites d et d’ et leur sécante $\Delta$ sont dits alternes internes.

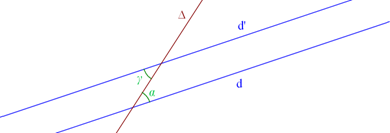
Si d // d’ alors $\alpha$ = $\gamma$
Réciproquement, si $\alpha$ = $\gamma$ , alors d // d’

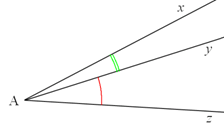
¤ Deux angles sont dits adjacents si :
– ils ont le même sommet
– ils ont un côté en commun
– ils sont situés de part et d’autre de ce côté commun
Exemple : $\widehat{{x} A{y}}$ et $\widehat{ {y} A{z}}$ sont adjacents
¤ Deux angles dont la somme des mesures vaut 90° sont dits complémentaires
¤ Deux angles dont la somme des mesures vaut 180° sont dits supplémentaires
¤ La somme des mesures des angles d’un triangle vaut 180°
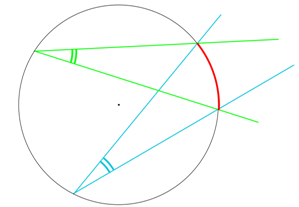
¤ Si deux angles inscrits dans un même cercle interceptent le même arc, alors ils ont la même mesure.

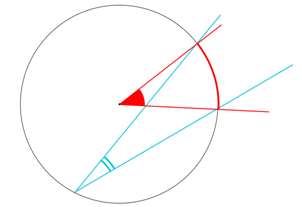
¤ Si, dans un cercle, un angle au centre et un angle inscrit interceptent le même arc, alors la mesure de l’angle au centre est le double de la mesure de l’angle inscrit.

¤ Dans un triangle rectangle,
– le cosinus d’un angle aigu est égal au rapport
$\frac{longueur\ du\ c\hat{o}t\acute{e}\ adjacent\ \grave{a}\ cet\ angle}{longueur\ de\ l’hypot\acute{e}nuse}$
– le sinus d’un angle aigu est égal au rapport
$\frac{longueur\ du\ c\hat{o}t\acute{e}\ oppos\acute{e}\ \grave{a}\ cet\ angle}{longueur\ de\ l’hypot\acute{e}nuse}$
– la tangente d’un angle aigu est égale au rapport
$\frac{longueur\ du\ c\hat{o}t\acute{e}\ oppos\acute{e}\ \grave{a}\ cet\ angle}{longueur\ du\ c\hat{o}t\acute{e}\ adjacent\ \grave{a}\ cet\ angle}$
Exemple : dans le triangle ABC rectangle en A

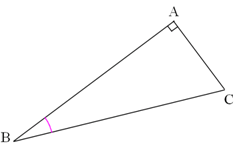
$\cos\widehat{ABC}$ = $\frac{AB}{BC}$
$\sin\widehat{ABC}$ = $\frac{AC}{BC}$
$\tan\widehat{ABC}$ = $\frac{AC}{AB}$

¤ Dans un triangle rectangle, quelle que soit la mesure ${x}$ d’un angle aigu :
$\tan{x} = \frac{\sin{x}}{\cos{x}}$
$\cos ^2 {x} + \sin ^2 {x} = 1$
Attention ! Le cosinus et le sinus de ${x}$ sont toujours compris entre 0 et 1 car l’hypoténuse est le plus grand côté du triangle rectangle.

¤ Dans un triangle, il y a
– 3 médianes : une médiane d’un triangle est une droite passant par un sommet du triangle et par le milieu du côté opposé à ce sommet.

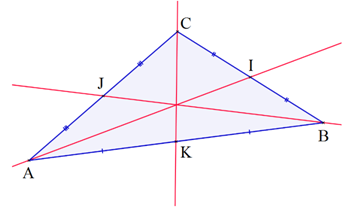
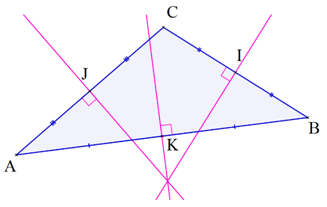
– 3 médiatrices : ce sont les médiatrices des 3 côtés, c’est-à-dire les droites qui coupent les côtés du triangles perpendiculairement en leur milieu.

– 3 hauteurs : une hauteur d’un triangle est une droite passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet.

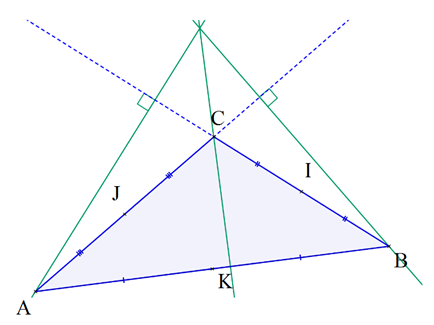
Ici, il a fallu prolonger le tracé des segments [AC] et [BC] pour construire les hauteurs issues de A et de B.
– 3 bissectrices : ce sont les bissectrices des 3 angles du triangles, c’est-à-dire les droites partageant les angles en deux angles adjacents de même mesure.

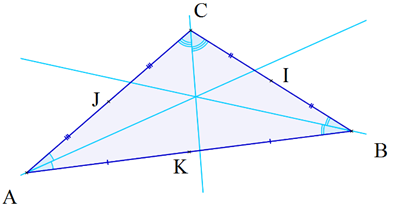
¤ Droite des milieux  :

– Dans un triangle, si une droite passe par les milieux de deux côtés, alors elle est parallèle au troisième côté.
– Dans un triangle, si une droite passe par le milieu d’un côté et si elle est parallèle à un deuxième côté, alors elle passe par le milieu du troisième côté.
– Dans un triangle, la longueur du segment qui joint les milieux de deux côtés et égale à la moitié de celle du troisième côté.

¤ Théorème de Thalès
Dans le triangle ABC, si M appartient à (AB), si N appartient à (AC) et si les droites (BC) et (MN) sont parallèles, alors $\frac{AM}{AB}$ = $\frac{AN}{AC}$ = $\frac{MN}{BC}$

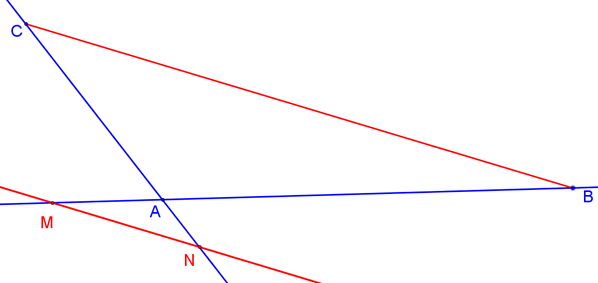
¤ Réciproque du théorème de Thalès
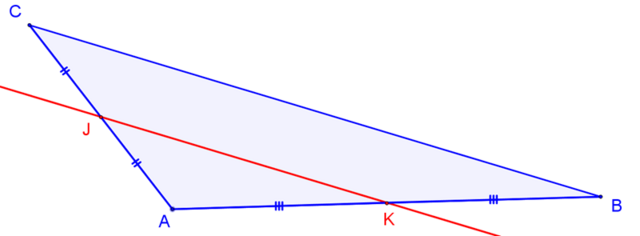
Dans un triangle ABC, si M et N sont deux points tels que A, B et M sont alignés dans le même ordre que A, C et N et si les rapports $\frac{AM}{AB}$ et $\frac{AN}{AC}$ sont égaux, alors les deux droites (BC) et (MN) sont parallèles.

¤ Théorème de Pythagore
Si ABC est un triangle rectangle en A, alors AB² + AC² = BC²

¤ Réciproque du théorème de Pythagore
Si dans le triangle MNP la relation MN² + MP² = NP² est vraie, alors on peut affirmer que le triangle MNP est rectangle en M.

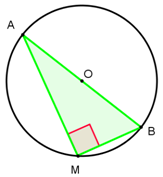
¤ Si le triangle ABM est inscrit dans le cercle de diamètre [AB], alors il est rectangle en M.